
WavebreakMediaMicro - Fotolia
How to calculate a subnet mask from hosts and subnets
IP addressing and subnetting are important and basic elements of networks. Learn how to calculate a subnet mask based on the required number of subnets and hosts.
A subnet mask is a number that specifies which parts of an IP address represent the host and network portions of the address. These masks are 32 bits in IPv4 networks and 128 bits in IPv6 networks.
A subnet mask is initially written in binary format, with network bits represented by ones and host bits by zeros. These binary numbers are typically converted to decimal format for convenience, however.
To calculate a subnet mask, network administrators determine the number of bits needed for both the network and host portions of an IP address. Once network admins determine the number of network bits, they set those bits to ones and the remaining bits to zeros for the host portion. They can then convert the binary format of the subnet mask to decimal.
While this process might seem impractical, IP addressing and subnetting are fundamental to networking, and network admins must understand how to apply this information to real-world scenarios. This article explains how to calculate a subnet mask using the host and subnet formulas.
What is subnetting and why is it important?
ISPs allocate IP address ranges to organizations based on the potential number of networks and hosts, or endpoints, that organizations require. These allocations follow the Classless Inter-Domain Routing (CIDR) assignment method.
Network administrators then subdivide the allocated address space into smaller allocations for each subnet within the organization, using a process called subnetting. Subnetting increases the number of subnets and decreases the number of usable host IP addresses. Each subnet is known as an IP subnet.
Network administrators create subnets for various reasons. Subnetting breaks network addresses into smaller, efficient allocations that are more suitable for each network within an organization. For example, a point-to-point WAN link between two routers needs only two addresses, while a LAN segment might need to support many hosts, such as servers, workstations, laptops and Wi-Fi-connected mobile devices.
Subnetting and route summarization work together to make routers more efficient by reducing the size of routing tables. Routers far away from a destination don't need much addressing detail, so routes can be summarized to a large degree.
As packets get closer to the destination network, routers need more local routing information, such as the local subnet mask. When routers apply the mask to a packet's destination address, they can determine which specific network segment contains the destination host and properly deliver the packet.
IP addressing and subnetting basics
Before you start to calculate subnet masks, you might want to start with a review of the basic elements of IP addressing and subnetting.
Essential information about IP addressing and subnetting includes the following:
- Unique IP addresses. IP addresses must be unique on the internet when using public IP addresses and on a private network when using private IP addresses.
- IPv4 and IPv6 address formats. IPv4 addresses are 32 bits, made up of four octets of eight bits each. To calculate the subnet mask, convert an IP address to binary, perform the calculation and then convert back to the IPv4 decimal number representation known as a dotted quad. The same procedure works for 128-bit IPv6 addresses.
- Subnet mask functionality. A subnet mask tells the computer which part of the IP address serves as the network portion of the address and which part identifies the host address range, which are addresses assigned to host computers on that network. A longer subnet mask -- which has more one bits in the mask -- creates more IP subnets that have a smaller host address block size.
- Subnet mask length. Subnetting breaks a large network into smaller networks by extending the length of the subnet mask. This increases the number of subnets and reduces the number of hosts per subnet. Organizations typically use several different subnet masks for different sizes of networks. For example, a point-to-point link with only two devices often uses a 31-bit mask. An office LAN or data center LAN, however, uses a shorter subnet mask that supports more hosts.
- IP address classes. Classless IP addresses with variable-length subnet masks are used almost exclusively today. In contrast, classful IP addresses -- known as either Class A network, Class B network or Class C network -- are used only for certification testing or older routing protocols. A Class D network is used for multicast, and Class E addresses are allocated for experimental purposes.
- Role of default gateways. A default gateway is a device, typically a router, where hosts send packets destined for a device that isn't on the local LAN. The gateway device uses its assigned subnet mask to compare its local IP address and subnet with the destination's IP address and subnet. This process helps the device determine what is -- and isn't -- on the local LAN.
- Private IP address use. Most networks use private IP addresses, also known as Request for Comment 1918 addresses. These IP addresses aren't routable over the internet and must be translated to public IP addresses to communicate on the internet, either through a proxy server or through port address translation .
How to calculate a subnet mask with the host's formula
A common, real-world question you might have when you lay out your network is, "What subnet mask do I need for my network?" To answer this question, you must know how to use the host's formula. The host's formula tells you how many hosts are allowed on a network that has a certain subnet mask.
The formula to calculate the number of hosts in a subnet is as follows:
2h - 2
The h represents the number of zeros in the subnet mask in binary format. The subtraction of 2 accounts for the first IP address in a subnet, which is reserved to identify the network, and the last IP address reserved as the broadcast address.
1. Find host range
To use the host's formula, let's first look at an example.
Suppose you plan to use the IP address space 192.168.0.0. Currently, you have a small network subnet with 20 hosts. This network will grow to 300 hosts within the next year, however, and you plan to have multiple locations of a similar size in the future and need to enable them to communicate using this address space.
With a single network subnet and only 20 hosts, the simplest thing to do is use 255.255.255.0 as your subnet mask. This means you have 192.168.0.1 through 192.168.0.254 for your hosts. The address 192.168.0.0 is reserved as the network subnet identifier, and 192.168.0.255 is reserved for the network broadcast address.
2. Convert to binary
Before you decide to use this subnet mask, apply the host's formula to it. To use the host's formula in this scenario, take the subnet mask 255.255.255.0 and convert it to binary. This gives you the following:
11111111.11111111.11111111.00000000
To find the number of hosts, use the host's formula:
2h - 2
The subnet mask has eight zeros, which means h equals 8, so you need to calculate 28 - 2.
28 - 2 = 256 - 2 = 254
Once you do the calculation, you have a result of 254. So, with the subnet mask specified, you have 254 usable hosts. This number of hosts suits a 20-user network now, but it won't support a future network expansion to 300 hosts.
3. Calculate the total number of hosts per subnet
Plan ahead and choose the best subnet mask to avoid having to go back later to change all the IP addresses on the network. If you add ones to the subnet mask, you have fewer hosts per network subnet, but more network subnets. If you remove ones from the subnet mask, you have more hosts per network, but fewer networks. The latter is what we need in this example.
To start, take away one of the ones to find the subnet mask:
11111111.11111111.11111110.00000000
This is 255.255.254.0 in dotted-decimal form.
Use the host's formula again:
2h - 2
The subnet mask has nine zeros, which means h equals 9, so you need to calculate 29 - 2.
29 - 2 = 512 - 2 = 510
This calculation results in 510 hosts. This suits a 20-user network now as well as future network and host expectations of 300 hosts.
The most efficient subnet mask for the network is 255.255.254.0. However, due to the limitations of writing the addresses as dotted quads, the valid host address range for each subnet must be written as two ranges.
The IP subnet ranges from 192.168.0.1 through 192.168.0.255, and the valid host addresses range from 192.168.1.0 through 192.168.1.254. The subnet address is 192.168.0.0, and the network broadcast address is 192.168.1.255.
That is how you arrive at the total of 510 usable hosts.
How to calculate a subnet mask with the subnet's formula
Once you understand the host's formula, you should also know the subnet's formula, which ensures you have the right subnet mask for the number of subnets that you have. Determining the right number of hosts for your LAN with the host's formula doesn't mean you have enough subnets for your network.
The subnet's formula is as follows:
2s
The s represents the number of ones added to the subnet mask, from whatever the subnet mask was.
Let's take the previous example and build on it.
If you expect to have 100 remote sites with 300 PCs each, with the network address 192.168.0.0, what subnet mask should you use?
In our last example, the 255.255.254.0 subnet mask provided 510 hosts per subnet. That was more than adequate to support 300 PCs, but does that same subnet mask provide networks for at least 100 remote sites?
Let's find out.
Verify the total number of subnets
You can find the number of subnets by counting the number of bits by which the initial mask was extended, also known as the subnet bits. Our initial address allocation was 192.168.0.0 with a mask of 255.255.0.0. The calculations found a subnet mask of 255.255.254.0 with the host's formula.
You can compare the two masks and count the subnet bits.
First, convert the masks to binary notation:
255.255.0.0 = 11111111.11111111.00000000.00000000
255.255.254.0 = 11111111.11111111.11111110.00000000
The new mask uses seven subnet bits, which means s equals 7, so you need to calculate 27.
27 = 128
Because this is at least 100, you have enough subnets for 100 remote networks. This is the right subnet mask for your network. If you convert the subnet mask from binary back to decimal, you get 255.255.254.0.
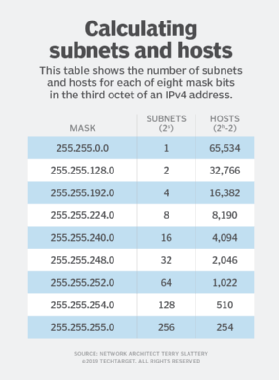
As you add subnet bits, the number of subnets increases by a factor of two, and the number of hosts per subnet decreases by a factor of two. Figure 1 shows the number of subnets and hosts for each of eight mask bits in the third octet of an IPv4 address.
How to calculate variable-length subnet masks
Most networks require several subnets of different sizes, sometimes called Variable Length Subnet Masks. You can create these subnets when you take one of the larger subnets -- a subnet with a shorter mask -- and apply the subnetting algorithm to it. This is known as variable length subnetting because the network has subnet masks of several different lengths.
Use the previous example and suppose that most of the 100 sites also require two point-to-point WAN links. This means you need 200 subnets with two hosts each -- a router on each end of the link.
Start with the subnet mask of 255.255.254.0 and use the host's formula to calculate for the number of hosts:
2h - 2
You need to reserve the network and broadcast addresses, and you need exactly two usable host addresses for the two point-to-point WAN links, which means the result must be 2. The only value for h that can satisfy the formula 2h - 2 = 2 is if h equals 2, or 22 - 2.
22 - 2 = 4 - 2 = 2
This calculation results in an extended subnet mask of 255.255.255.252, with 30 network bits and only two host bits.
Let's compare the original and extended subnet masks in binary:
255.255.254.0 = 11111111.11111111.11111110.00000000
255.255.255.252 = 11111111.11111111.11111111.11111100
Binary form indicates the subnet mask has been extended by seven bits. Next, use the subnet's formula to determine the number of available subnets.
2s
In this example, s equals 7, resulting in the following calculation:
27 = 128
This equation gives you 128 subnets, but that isn't enough for all our WAN links, of which you need 200. You need to subnet another large subnet to have enough links. If you sub-subnet the top two large subnets for WAN links, you have enough capacity for 256 point-to-point links, which satisfies the 200-link requirement.
Let's look at the following subnet ranges:
192.168.252.0 through 192.168.253.254 provides the IP range for WAN subnets 0 through 127.
192.168.254.0 through 192.168.255.254 covers WAN subnets 128 through 255.
You can use the same process if your organization has many small remote sites that have few hosts at each site, such as in a retail business. Remember to assign subnets to sites in a way that enables address summarization to reduce routing table size and increase router efficiency.
Support for 31-bit masks
Modern routers also support using a 31-bit subnet mask, or 255.255.255.254, for point-to-point links because point-to-point links don't need broadcast addresses. This configuration is an exception to the rule that reserves two addresses to identify the subnet and act as the broadcast address.
CIDR notation
CIDR eliminates the original classful designation of IPv4 addresses. It enables a single network prefix and mask to represent an aggregation of multiple networks. This is also called supernetting. CIDR address representation simplifies the representation of an address and mask. CIDR also supports network aggregation and address summarization.
CIDR notation appends the number of subnet mask bits to the network address, using a forward slash (/) and the number of bits in the subnet mask.
In the previous example of 100 subnets that support over 300 hosts each, the subnet mask contains 23 bits, as determined by the number of consecutive ones in the binary form of the subnet mask. The total number of ones indicates the prefix length of the network.
| IP address | Subnet mask | CIDR notation | |
| Decimal | 192.168.0.1 | 255.255.254.0 | 192.168.0.1/23 |
| Binary | 11000000.10101000.00000000.00000001 | 11111111.11111111.11111110.00000000 |
Calculate the subnet prefix
Routers calculate the subnet address as part of the process to determine which interface to use to forward packets to their destination. This process uses a binary AND operation on an address and its mask. The result is the subnet prefix, which removes all the host bits.
The router uses the network prefix to find the routing table entry that best matches the prefix -- the longest match or the default route. The packet is forwarded out of the interface that is associated with the best match prefix.
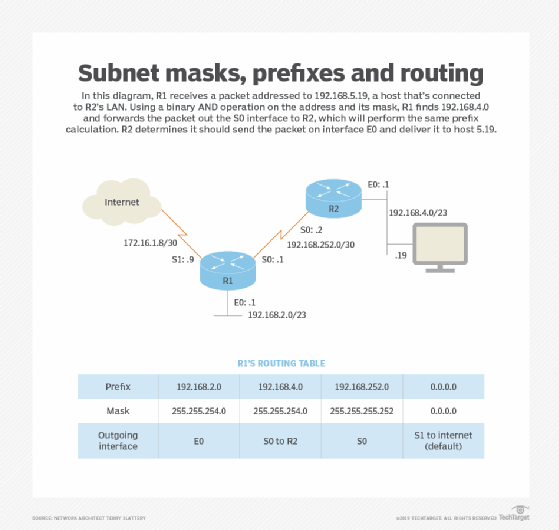
In Figure 2, suppose R1 receives a packet addressed to 192.168.5.19, a host that is connected to R2's LAN. Use the binary AND operation between the mask and the address to determine the route prefix to look up in the routing table:
192.168.5.19 = 11000000.10101000.00000101.00010011
255.255.254.0 = 11111111.11111111.11111110 00000000
192.168.4.0 = 11000000.10101000.00000100.00000000
R1 finds 192.168.4.0 in the routing table and forwards the packet out the S0 interface to R2. R2 does the same prefix calculation and determines that it should send the packet on to interface E0 and that it is a local delivery to host 5.19.
Understand large-scale network design
In the real world, you probably won't have the chance to design a large network such as this from scratch. If a time comes when you need to design a network from scratch, you'll likely be able to verify your calculations with a subnet calculator.
However, it's still important to understand subnetting and be able to calculate masks, host ranges and subnets longhand. Large-scale network design skills are valuable for various reasons, including the following:
- Understand network configuration. Network design skills help network administrators understand how to subnet an existing large-scale network.
- Learn the effects of changes. Network design skills help administrators understand how network modifications, such as changes to a network or its IP addressing and subnetting configurations, could affect performance.
- Satisfy certification requirements. Network certification exams sometimes require practitioners to calculate IP addressing without a calculator to prove they understand and can apply IP addressing and subnetting skills.
Editor's note: This article was originally written by David Davis and updated by Terry Slattery and TechTarget editors to expand coverage and improve the reader experience.
Terry Slattery is an independent consultant who specializes in network management and network automation. He founded Netcordia and invented NetMRI, a network analysis appliance that provides visibility into the issues and complexity of modern router- and switch-based IP networks.
David Davis is a virtualization and cloud computing expert, author and speaker with video training content available on Pluralsight.com and LinkedIn.com/Learning.






